渥太华 / 肖庆涵
题记:1971年夏天,邮电部阳新五七干校的中学里,来了一位戴眼镜的新同学。放学后我回去告诉妈妈,一排今天来了一个叫张益唐的同学,在看一本厚厚的数论方面的书呢。妈妈告诉我,张益唐的母亲也是从上海调到北京邮电部的,并讲了个他母亲如何激励张益唐学习的故事。上个月16号干校同学群中传出,张益唐已证明黎曼猜想相关问题的好消息。特写成此文,希望能为普通人了解这项工作提供一些帮助。
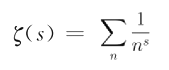
最近有关传奇数学家张益唐教授,攻克朗道-西格尔零点猜想的消息,引发了广泛的关注。首先是他举行的在线讲座和学术报告,然后是他在arXiv上将论文正式公开,不仅引发了学术界的关注,而且在网络上也是火爆刷屏。由于网上的不少文章,写的人也没弄懂朗道-西格尔零点猜想到底是怎么回事,所以除了赞誉之词外,大家读完之后会是一头雾水。因此萌发出应该写一篇短文,让有兴趣的普通人看了也能明白,什么是朗道-西格尔零点猜想?张益唐要证明什么?这项工作的意义何在?等等。
这件事还要从伟大的数学家欧拉(1707-1783)说起,他曾经研究过如下的无穷级数:
这个级数实际上是s的函数,后来被称为ζ函数。几十年后高斯的学生黎曼(1826-1866)将欧拉的ζ函数,解析延拓到几乎整个复平面(除了s=1),解析延拓后的ζ函数叫做“黎曼ζ函数”。黎曼注意到,ζ函数的零点有两种。当s=-2、-4、-6、-8…(负偶数)时,是平凡零点,其它零点则被黎曼称为非平凡零点。
而著名的黎曼猜想说的是:所有的非平凡零点都在实部等于二分之一的那条垂直线上。黎曼猜想公布44年后,数学家第一次算出了前15个非平凡零点,又过了20年,算出了前138个非平凡零点。之后数学家西格尔在黎曼手稿中,发现了一个黎曼计算非平凡零点的公式,数学界称为黎曼-西格尔公式。用此公式,西格尔在4年内算出了1000多个非平凡零点。目前数学家们用计算机依据黎曼-西格尔公式,验证了前200多亿个非平凡零点,它们的实部全都是0.5,无一例外。
1837年德国数学家狄利克雷,引进了狄利克雷L函数。狄利克雷L函数可以看作是黎曼ζ函数的推广(被称作广义黎曼猜想)。在黎曼猜想中,黎曼ζ函数的所有非平凡零点都在直线½+ti上;在广义黎曼猜想中,狄利克雷L函数的所有非平凡零点都位于复平面上Re(s) = ½的直线上。朗道(1877-1938)和西格尔(1896-1981),是两位德国数学家,朗道是西格尔的导师。他们对狄利克雷L函数的非平凡零点进行了深入的研究,发现满足特殊性质时,其对应的L函数可能出现位置异常的零点,异常的零点並非位于实部1/2的那条直线上,而是在非常靠近1的地方。这个零点就被称为“朗道-西格尔零点”,因此朗道-西格尔零点被定义为广义黎曼猜想的反例。如果这个零点真存在的话,广义黎曼假设就错了。张益唐这次的论文就是试图证明朗道-西格尔零点不存在。
在数论研究中,筛法是数论中的一类基本方法,其研究对象是筛函数。筛法的原理就是从一个集合中筛去特殊的元素,并估计剩余元素的数量。1950年前后,塞尔伯格利用求二次极值的方法,对古老的筛法作出了一项重大改进,因此这种筛法被称为“塞尔伯格筛法”,它成为数论研究中的重要工具并被沿用至今。当年陈景润曾使哥德巴赫猜想前进了一大步,近年张益唐解决孪生素数猜想和这次的论文,其思路都是受塞尔伯格筛法的启发。张益唐在北大读研究生时的导师潘承彪教授听了张益唐的报告后评论说:“听了益唐讲的想法很清楚,这是一个重要的筛法新思想,有很大发展潜力,可实现起来很难”。究其原因,是涉及到的误差项,只能一个一个做、一个一个去估计,然后把最终的结果控制在一个小的范围之内。张益唐论文中这个数是2024,如果把2024换成1,得到的就是原始形式的朗道-西格尔零点猜想了。所以,对这篇论文如何评价,还要等国际上同行们的评议和学术界对论文中公式推导的检验。
在国际数学界看来,华裔甚或是亚裔数学家,所涉猎的大多是二流或三流的数学问题。陈景润1+2的证明,被公认是一个十分杰出的成果,是对哥德巴赫猜想研究的巨大贡献。但沿着陈氏定理的“加数筛法”,大概无法最终解决哥德巴赫猜想。而张益唐把孪生素数猜想从无穷变为有限,和这次对朗道-西格尔零点猜想的冲击,无疑都是一流的数论问题。衷心希望他的论文是正确的,这将使国际数学界对中国的数学界刮目相看,毕竟大家都很清楚,张益唐的数论不是在普渡大学里学成的。